Simulation of group selection models

Group selection theory studies a genetically inherited trait, called altruism, which increases the fitness of a group of individuals, but decreases the fitness of the individual carrying this trait. Group selection will promote the gene for altruism, while individual selection will tend to eliminate it. Which of these two opposing forces will win is a very controversial question in sociobiology. The Altruist software package has been developed to simulate various models of group selection in order to determine under which conditions altruism or egoism will prevail.

Several different models of group selection are simulated with the Altruist software package:

Island model: A species lives on an archipelago where migration between the islands is rare. Occasionally, the group inhabiting an island goes extinct and the island is re-colonized by migrants from one or more other islands. The more altruists there are in a group, the lower the probability that the group is extinguished. Various variants of the island model assumes that immigrants come only from neighbor islands, from any island with equal probability, or from an imaginary pool of migrants having the same genetic composition as the metapopulation. The group of colonists occupying a deserted island may either all come from the same neighbor group (fission) or have mixed origin.
Founder effect: This is similar to the island model, but extinction happens mainly to small new-formed groups. The extinction rate may be very high so that only few new colonies survive and grow.
Intrademic group selection: This is also called the haystack model. The scenario in this model is that mice live in a field full of haystacks. Each haystack houses a group of mice. Altruists benefit the group they live in, in such a way that the whole group breeds faster, while the altruists themselves breed less than egoists in the same group do. After a few generations the haystacks are removed and all the mice mix up. The groups that contain many altruists will contribute more to the metapopulation than groups with few altruists when the haystacks are removed. Next year a new set of haystacks is set up and the process is repeated.
Viscous population model: The population need not be divided into well-defined demes, as long as it is viscous. Individuals living in areas with a high fraction of altruists have a higher fertility or are able to utilize resources better than in areas with few altruists, and hence there will be a higher rate of migration from areas with many altruists to areas with few altruists than vice versa.
Group territoriality model: A species lives in groups and each group has a territory which it defends. Altruists invest more than egoists do in defending their territory and conquering new territory from neighbor groups. This is costly for the altruist but benefits the whole group. A group with many altruists will steal territory from neighbor groups with fewer altruists. When a group thus becomes too big it will split up into two groups. Other groups that get too small may perish or become absorbed by neighbor groups.

My simulations show that intrademic group selection and the viscous population model are very vulnerable to individual selection, but resistant to migration. The island model is considerably stronger, but cannot withstand a high migration rate. A founder effect may speed up group selection, but is not very resistant to migration and back mutation unless it is combined with one of the other mechanisms. The group territoriality model is the strongest. The latter model has not been analyzed before although it appears to be very realistic.

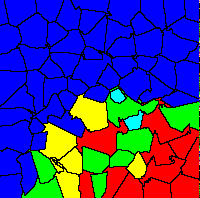This picture shows an example of group selection in the group territoriality model. The colored areas show group territories with different genetic compositions:
       blue: mainly egoists, 0 - 20 % altruists
       cyan: 20 - 40 % altruists
       green: 40 - 60 % altruists
       yellow: 60 - 80 % altruists
       red: 80 - 100 % altruists

Group selection is obviously very sensitive to the rate of migration between groups. A single egoist migrating into a group of altruists may breed so that eventually, after many generations, the group consists of only egoists. I have therefore made a series of simulations to determine the highest migration rate that the altruism gene can withstand under various conditions. The following figures show limiting migration rates as a function of average group size for various models.

model	dominance of altruism gene		parameters
model	recessive	dominant	parameters
group territoriality model, migration restricted to neighbor groups		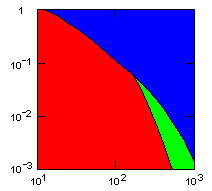	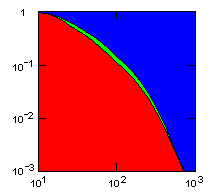Individual selection: 5% Growth rate: 1.5 Number of groups: 1000 Average group size: 100 Group fitness exponent: 1 Product factor: 0.1 Border factor: 0.2 Random factor: 0.01.
island model, migration restricted to neighbor islands, new colonies formed by group fission		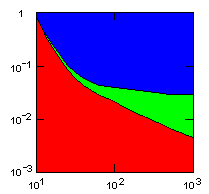	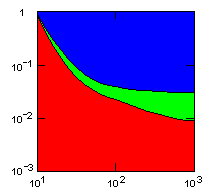Individual selection: 5% Growth rate: 1.5 Number of islands: 1000 Average carrying capacity of islands: 100 Average size of new colonies: 8 Group fitness exponent: 1 Probability of deme extinction: egoist demes: 0.1, altruist demes: 0.01
island model, migration restricted to neighbor islands, new colonies formed by migrants that may come from all neighbor groups.		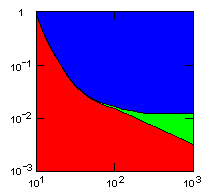	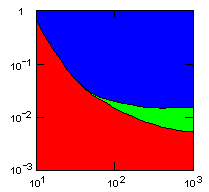do.
island model, no geographic restraints on migration		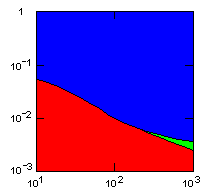	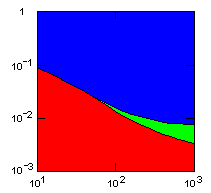do.
Parameter maps showing simulation results as a function of parameters: x-axis: average size of (full-grown) groups y-axis: migration rate Color code: red: fixation of altruism gene blue: fixation of egoism gene green: stable polymorphism

Another factor that has a considerable influence, although less obvious, is how the group fitness depends on the fraction of altruists. This is modeled by the function:

(group fitness) = (fraction of phenotypic altruists) ^{(group fitness
exponent)}

A group fitness exponent below one means that a group of half egoists and half altruists has a group fitness that is more than midway between that of all-egoist groups and all-altruist groups. A group fitness exponent above one, on the other hand, means that a mixed group has relatively low group fitness.

The following figures show limiting migration rates as a function of the group fitness exponent for various models.

model	dominance of altruism gene		parameters
model	recessive	dominant	parameters
group territoriality model, migration restricted to neighbor groups		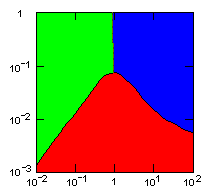	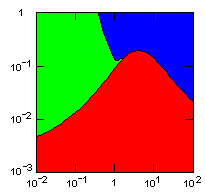Individual selection: 5% Growth rate: 1.5 Number of groups: 1000 Average group size: 100 Group fitness exponent: 1 Product factor: 0.1 Border factor: 0.2 Random factor: 0.01.
island model, migration restricted to neighbor islands, new colonies formed by group fission		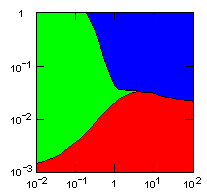	Individual selection: 5% Growth rate: 1.5 Number of islands: 1000 Average carrying capacity of islands: 100 Average size of new colonies: 8 Group fitness exponent: 1 Probability of deme extinction: egoist demes: 0.1, altruist demes: 0.01
island model, migration restricted to neighbor islands, new colonies formed by migrants that may come from all neighbor groups.			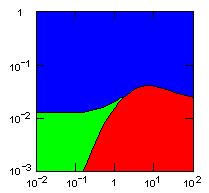do.
island model, no geographic restraints on migration		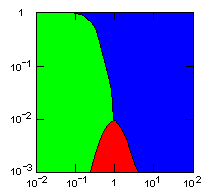	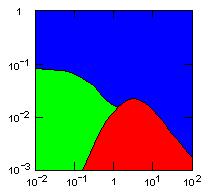do.
Parameter maps showing simulation results as a function of parameters: x-axis: group fitness exponent y-axis: migration rate Color code: red: fixation of altruism gene blue: fixation of egoism gene green: stable polymorphism

Previous quantitative studies of group selection have mainly used mathematical analysis. Various assumptions and approximations have been necessary to make the models mathematically tractable (e.g. Boorman & Levitt 1980). My simulation studies show that many of these approximations are inadmissible. For example, many models ignore migration, and most models ignore geographic constraints on migration. The figures above show that the migration rate is very important, and that the assumption of random migration makes group selection seem much less effective than it is when there are geographic restraints on migration. The simulations also show that interdemic group selection is much stronger than intrademic group selection, although many contemporary theorists (e.g. Reeve & keller 1999) favor only the latter model.

A further advantage of simulation over mathematical analysis is that it makes it possible to study more realistic models like the group territoriality model.

Since group selection is most effective under low migration rates, the question arises of how a low migration rate can evolve when there are no physical barriers to migration, as in the group territoriality model. This question has been answered by a theoretical analysis showing that a gene that lowers the rate of migration into a group can evolve simply because it prevents the spread of competing genes (Peck 1990). This finding has been confirmed by my simulation studies. In fact, simulation of the endogamy model, which includes a locus for endogamy and a locus for altruism, shows that the altruism gene spreads geographically on the heels of the endogamy gene.

Conclusion

The simulation methods applied here enable the study of more detailed and realistic models of group selection than previously possible. It shows that group selection is able to override counteracting individual selection under a much broader range of conditions than previously believed, especially for the more realistic group territoriality model. This brings the theory more in accordance with observations of eusociality in species like termites and naked mole rat (Thorne 1997, Jarvis 1981) and may even explain altruistic traits in the human psyche.

The results are briefly described in Fog (2000).

References

Boorman, S A; Levitt, P R (1980): The Genetics of Altruism. New York: Academic Press.

Jarvis, J U M (1981): Eusociality in a mammal: Cooperative breeding in naked mole rat. Science vol. 212 1981 p 571-573.

Peck, J R (1990): The Evolution of Outsider Exclusion. Journal of theoretical Biology, vol. 142, no. 4, pp. 565-571.

Reeve, H K & Keller, L (1999): Levels of Selection: Burying the Units-of-Selection Debate and Unearthing the Crucial New Issues. In: Keller, L (ed): Levels of Selection in Evolution. Princeton University Press.

Thorne, B L (1997): Evolution of eusociality in termites. Annual Review of Ecology and Systematics, no. 28, pp. 27-54.

Fog, A (2000): Simulation of Evolution in Structured Populations: The Open Source Software Package Altruist. Biotech Software & Internet Report. Vol. 1, No. 5, p. 226-229.